剑指 Offer 11. 旋转数组的最小数字

原题链接

题目描述：

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。  

注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

示例 1：

输入：numbers = [3,4,5,1,2]
输出：1

示例 2：

输入：numbers = [2,2,2,0,1]
输出：0

以下二分均指整数二分：

谈及二分，很多人的认识是二分必须满足单调性，二分搜索只能在有序数组上进行，然而并非如此，正如本题，可能很多人都能用二分的方法做出来，但若你问这不是不满足单调性吗？或许就很少有人能回答些许了。而二分与单调的关系实则应是这样的：

单调一定可以二分，二分不一定要单调。

二分的本质并非是单调性，而是边界。

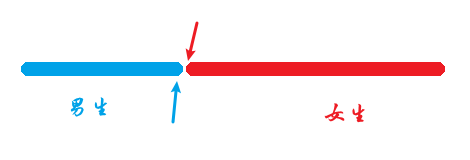
比如有一个队伍，前面都是女生，后面都是男生，很显然，本题也可以采用二分的方式来寻找男女生的边界，可以找到男生的第一位同学，同样也可以找到女生的最后一位同学，实现不同的check（）函数即可完成两种方案。

所以总结一下，二分有两个必要的因素，

1. 有边界情况；
2. 是在算法中能对边界两侧情况进行check（）。

那么本题这两个因素分别是什么呢？

本题的难点也就在这一点，或许还是不太清晰，让我们再加上一笔。

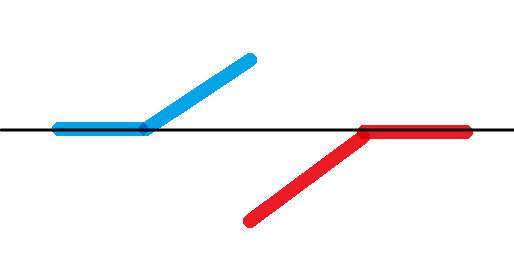
发现了吗？没错，假如我们先忽略掉与黑线相等的数值，那么蓝色与红色的数值就有了边界，也就是黑线数值，同时也很好check（），所以我们要做的只是去掉红色或蓝色与黑线相等的值，使其满足二分条件即可，本题解决。

我的代码：

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int l = 0, r = numbers.size() - 1;
        // 为满足二分条件，去除末尾与开头相同元素
        while(r >=0 && numbers[l] == numbers[r])
            r --;
        // 特判全部为一个数字
        if(l == r)
            return numbers[0];
        // 特判整个旋转情况
        if(numbers[0] < numbers.back())
            return numbers[0];
        
        int target = numbers[0];
        while(l < r)
        {
            int mid = l + r + 1 >> 1;
            if(numbers[mid] >= target)
                l = mid;
            else
                r = mid - 1;
        }
        return numbers[r + 1];
    }
};