启发性信息和评估函数
如果在选择节点时能充分利用与问题有关的特征信息,估计出节点的重要性,就能在搜索时选择重要性较高的节点,以利于求得最优解。这个过程称为启发式搜索。
与被解问题的某些特征值有关的控制信息(如解的出现规律、解的结构特征等)称为搜索的启发信息。它反映在评估函数中,评估函数的作用是评估待扩展各节点在问题求解中的价值,即评估节点的重要性。
评估函数 : f(x) = g(x) + h(x)
g(x)是从初始节点到一个节点x的实际代价。
h(x)是这个节点x到目标节点的最优路径的估计代价,体现了问题的启发式信息,h(x)称为启发式函数。
启发式搜索算法 A算法
如果OPEN表是用评估函数f(x)来排序,找到最先/优/小出表的节点,就称为A算法。
搜索算法的可采纳性(Admissibility)和A*算法
如果搜索法总能找到最短(代价最小)的解答路径,则称算法具有可采纳性。宽度优先搜索就是可采纳的,只不过效率不高。
可采纳性/可容纳性/可容
h(n) <= h’(n)
其中h’(n)是实际代价,h(n)是估计代价 – 保证了可采纳性
A*算法的步骤为:
1.把S放人OPEN表,记f=h,令CLOSE为空表。
2.若OPEN为空表,则宣告失败并退出 。
3.选取OPEN 表中未设置过的具有最小f值的节点为最佳节点BESTNODE,并把它放人CLOSE表。
4.若BESTNODE为一目标节点,则成功求得一解并退出。
5.若BESTNODE不是目标节点,则扩展之,产生后继节点SUCCSSOR。
6.对每个SUCCSSOR进行下列过程:
- ①建立从SUCCSSOR返回 BESTNODE的指针;
- ②计算g(SUC)=g(BES)+g(BES,SUC);
- ③如果SUCCSSOR ∈ OPEN,则此节点为OLD,并把它添至BESTNODE的后继节古表中;
- ④比较新旧路径代价。如果g(SUC) < g(OLD),则重新确定OLD的父辈节点为BESTNODE,记下较小代价g(OLD),并修正f(OLD)值;
- ⑤若至OLD节点的代价较低或一样,则停止扩展节点;
- ⑥若SUCCSSOR不在OPEN表中,则看其是否在CLOSE表中;
- ⑦若SUCCSSOR在CLOSE表中,则转向③步骤;
- ⑧若SUCCSSOR既不在OPEN表中,又不在CLOSE表中,则把它放人OPEN 表中,并添人BESTNODE后裔表,然后转向第(7)步
7.计算f值,然后转人第(2)步 。
启发式函数的强弱及其影响
可以用h(x)接近h*(x)的程度去衡量启发式函数的强弱。
当h(x) < h*(x)时,h(x)过弱,从而导致OPEN表中节点排序的误差较大,易于产生较大的搜索图。
当h(x) > h*(x)时,h(x)过强,使算法A*失去可采纳性,从而不能确保找到最短解答路径。
当h(x)=h* (x) 最为理想,其确保产生最小的捜索图(因为OPEN表中节点的排序正确)且捜索到的解答路径是最短的。
但设计h(x)=h* (x)是不可能的,因此设计接近,又总是h(x) <= h*(x)成为应用A*算法捜索问题解答的关键。
h(x) <= h*(x) •h(x)包含的(启发式)信息越多越好,越接近h*(x)越好 •可以由N多个h(x)的设计方案,效果最好的那个,就是A*算法的,其他的都可以当是A算法的。
设计h(x)的实用考虑
对于评价函数f(x) = g(x) + h(x)
如果h(x) = 0, 搜索接近于宽度优先搜索
如果g(x) = 0, 搜索接近于深度优先搜索
加入一个权值ω使f(x) = g(x) + ωh(x)
当浅层时,使ω取值较大,使g(x)占比小,突出启发函数,加速纵向(深度)搜索
当深层时,使ω取值较小,使g(x)占比大,加速横向(广度)搜索
迭代加深A*算法: IDA*
设置一个限制值 c
只有当节点n的子节点n’的f(n’) < c时,才扩展n’节点放到栈中,并且更新c的值(取它和f(n’)较小的那个值)
算法终止的条件是: •找到目标节点 •栈为空并且限制值c’= ∞ (可以理解成是一个巨大的值,如100000000)
使用IDA*是为了优化空间,节省内存。
示例:
用启发式搜索算法A或者A*解决下面的八数码问题,并给出搜索结束时OPEN表和CLOSE表内容
评价函数 f(x) = g(x) + h(x)
其中h(x)的含义可以自己定义
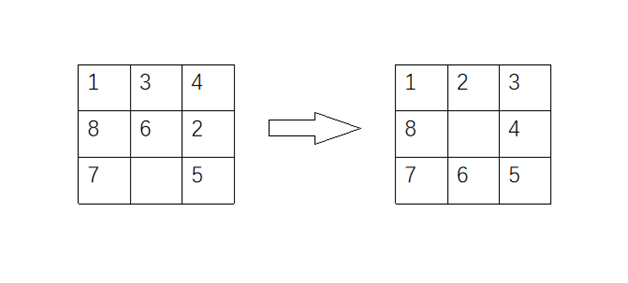
设
h(n):已经移动的步数
g(n):此状态与目标状态九宫格中相异数字的个数
代码:
import copy
start = ['1','3','4','8','6','2','7','x','5']
end = ['1','2','3','8','x','4','7','6','5']
#start = input().split()
#end = input().split()
start = [start[0:3], start[3:6], start[6:9]]
end = [end[0:3], end[3:6], end[6:9]]
open = []
close = []
def value_Fx(hx, start): # 求Fx
global end
gx = 0
for i in range(3):
for j in range(3):
if(start[i][j] != end[i][j]):
gx += 1
return gx + hx
def search_Position(lst):
position = (-1, -1)
for i in range(3):
if "x" in lst[i]:
position = (i, lst[i].index('x'))
return position
def find_Next(orient, hx, A0):
next = copy.deepcopy(A0)
position = search_Position(next)
#print(position)
# orient 代表拓展节点的方向,上下左右
if orient == 1:
next_position = (position[0]-1, position[1])
if orient == 2:
next_position = (position[0]+1, position[1])
if orient == 3:
next_position = (position[0], position[1]-1)
if orient == 4:
next_position = (position[0], position[1]+1)
if (next_position[0] < 3 and next_position[1] < 3 and next_position[0] >= 0 and next_position[1] >= 0):
next[position[0]][position[1]], next[next_position[0]][next_position[1]] = next[next_position[0]][next_position[1]], next[position[0]][position[1]]
return [next, value_Fx(hx, next)]
else:
# return (next,10) # 取10就是最大值了,存入不需要处理,后续用False代替
return False
hx = 0
position = search_Position(start)
#print(position)
open.append([start,value_Fx(hx, start)])
while True:
hx += 1
if not open: # Open表空失败退出
print("No answer!")
A = open.pop() # A是带fn的
close.append(A)
if A[0] == end: # 判断A是否目标节点
# print(close)
break
for i in range(1,5):
A_Next = find_Next(i, hx, A[0])
if A_Next: # 保证合法
lst = [i[0] for i in open]
lst += [i[0] for i in close]
if(A_Next[0] not in lst):
open.append(A_Next) # 两表中都不存在的节点存入open表中
else:
pass
open = sorted(open, key = lambda x:x[1], reverse = True) # reverse = True 降序排列,第一个节点使用pop取出即可
print("close表内容:")
for i in close:
print(i[1])
for j in i[0]:
print(j)
print("open表内容")
for i in open:
print(i[1])
for j in i[0]:
print(j)运行结果:









Comments NOTHING